Month: September 2025

The Texas Rangers have about a 1 in 4000 chance of making the playoffs

tomisphereLeave a comment

If you look at the playoff odds on FanGraphs.com right now, you’ll see the Texas Rangers listed as having a 0.0% chance of making the playoffs this year. But that doesn’t mean they have no chance. It just means their chance is so small that it doesn’t round up to 0.1%; instead it rounds down to 0.0%, as any chance less than 1 in 2000 will do. As it turns out, their chance of making the playoffs is about 1 in 4000 right now.

How we get to that number involves a lot of logical reasoning, complicated by the fact that the Rangers will play a series against one of the four teams they’re chasing, and there will be two series played this week between some of those same four teams.

Let’s set the stage properly. Here are the 8 remaining playoff contenders in the American League:

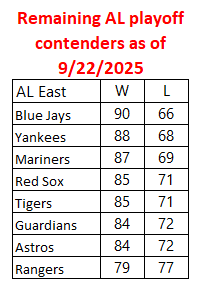
Only 6 teams in the American League may go to the playoffs. To be one of those 6, the Rangers must pass 2 of the 7 teams ahead of them in the standings (so long as one of them is not a division winner). Fortunately for the Rangers, there are 4 teams they still have a chance to reach. Unfortunately, they’ll be very difficult to reach.

Notice that if the Rangers win all 6 of their remaining games, and the Red Sox lose all 6 of theirs, that the Rangers would only manage to be tied with the Red Sox. But because they hold the tiebreaker over the Red Sox (having won 4 of the 7 games played between them this year), the Rangers would beat out the Red Sox in that case.

The same goes for Detroit. The Tigers must lose all 6 of theirs, and the Rangers must win all 6 of theirs, for the Rangers to tie; because they win the tiebreaker (having won 4 of 6 against the Tigers), the Rangers would beat out the Tigers.

The Rangers did not win their season series against the Astros, however, so must beat them by a game in the final standings, to pass them for a playoff spot. Because they are currently 5 games behind them, that could only happen if the Rangers win all 6 of their remaining games, and the Astros lose all 6 of theirs.

For the Rangers to catch the Guardians, they’ll have to win some of their remaining 3 games against them; those wins would give the tiebreaker to the Rangers. So the Rangers could stand to lose 1 game, or could stand the Guardians winning 1 game, and still beat them for a playoff spot.

Given that there’s only 1 team that isn’t forcing the Rangers to win all their remaining games, but that they need to beat at least 2 of these teams, the only option for the Rangers is to win all their remaining games.

Let’s start a list of requirements like this one:

We’re assuming here that every game a team plays the rest of the way has a 1/2 chance of being a win, and a 1/2 chance of being a loss. Because the Rangers have 6 games remaining, and there’s only 1 way to achieve the stated outcome (Rangers win all 6), that’s 1 outcome out of 26 possible outcomes, or a 1/64 chance of it happening.

What other outcomes must we consider?

Well if none of these teams were playing each other in these final 6 games, it would be a little less complicated. All the outcomes would be independent, so we could calculate the odds of each team’s win totals independently, as a starting point. Our list of requirements would look like this:

Because the Rangers would have to beat at least 2 of these teams, we’d take pairs of outcomes and calculate their odds:

[ (Red Sox lose all) AND (Tigers lose all) ]
OR [ (Red Sox lose all) AND (Astros lose all) ]
OR [ (Red Sox lose all) AND (Guardians lose 5 or 6) ]
OR [ (Tigers lose all) AND (Astros lose all) ]
OR [ (Astros lose all) AND (Guardians lose 5 or 6) ]

Notice that we didn’t include (Tigers lose all) AND (Guardians lose 5 or 6). That’s because one of those teams will win the central division; beating a division winner doesn’t help you win a wild card spot. They have to beat at least one of the Red Sox or Astros to get into the playoffs.

So we would multiply odds everywhere there’s an AND above, and then add them everywhere there is an OR above.

This would double-count or triple-count some cases though. For example, it would triple count the case where all three of these occur: (Red Sox lose all) AND (Tigers lose all) AND (Astros lose all). We’d have to subtract out double the odds of that happening.

After making a few more adjustments where 3 of those occur, we’d probably have one final adjustment to make for the case where all 4 occur:

(Red Sox lose all) AND (Tigers lose all) AND (Astros lose all) AND (Guardians lose 5 or 6).

Then we’d multiply our result by the odds of the Rangers winning all their games, because that has to happen in every case of the Rangers making the playoffs.

But we don’t live in that world. We live in a world where, in the final games of the season:

The Tigers play 3 games against the Red Sox
The Tigers play 3 games against the Guardians
The Rangers play 3 games against the Guardians

Oh my. This reduces the number of games that determine the Rangers’ fate from 30 down to 21. That’s good for the Rangers, because it means a lot fewer games would have to go a certain way for them to make the playoffs, and that gives them better odds.

It also changes how we do this. Now the outcomes we need to consider look like this:

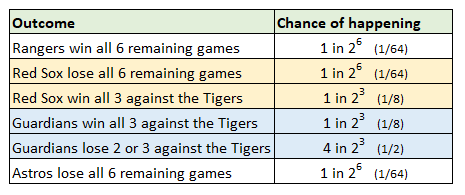
I’ve used highlighting to show outcomes that are related to each other in that they cannot both happen. For example, looking at the two lines in gold, we see that the Red Sox cannot simultaneously lose all their remaining games while also winning all 3 against the Tigers.

Let’s consider those two middle lines right now. If the Tigers lose all their remaining games, that means both the Red Sox and Guardians win at least 3 games. And that means the Rangers can’t beat either of those teams. The only team left that they could beat is the Astros. So if the Rangers beat the Tigers, they must also beat the Astros (and only the Astros) to get into the playoffs. That gives us this:

(Tigers lose all) AND (Astros lose all)

Which is actually this:

(Red Sox win all 3 against the Tigers) AND (Guardians win all 3 against the Tigers) AND (Astros lose all)

And there is no chance of double-counting with other outcomes. This will very much simplify our work to compensate for double countings.

To this we add the following:

[ (Red Sox lose all) AND (Astros lose all) ]
OR [ (Red Sox lose all) AND (Guardians lose 5 or 6) ]
OR [ (Astros lose all) AND (Guardians lose 5 or 6) ]

But consider that in the end we’ll be multiplying everything by the odds of (Rangers win all), which must happen in every scenario. Because the Rangers play 3 of those games against the Guardians, that means three of the Guardian’s losses have already been accounted for by the (Rangers win all) outcome. So we only need to consider the additional chance that the Guardians lose 2 or 3 against the Tigers. So the above becomes:

[ (Red Sox lose all) AND (Astros lose all) ]
OR [ (Red Sox lose all) AND (Guardians lose 2 or 3 to Tigers) ]
OR [ (Astros lose all) AND (Guardians lose 2 or 3 to Tigers) ]

Notice that in all 3 of these scenarios, the Tigers become unreachable to the Rangers, because they win at least 2 games. The only double or triple counting in this trio of scenarios is where the Rangers beat everyone but the Tigers:

(Red Sox lose all) AND (Astros lose all) AND (Guardians lose 2 or 3 to Tigers)

That’s a triple-count, so we have to subtract double the odds of that happening.

We can put all this together, with odds, in a new chart:

We add the first four lines then subtract 2 times the last line to compensate for double counting:

2-12 + 2-12 + 2-7 + 2-7 – 2 x 2-13 = 2-6 + 2-12 = 65/4096.

Which we multiply by the odds of the Rangers winning all 6 of their remaining games, to give 65/262144. That’s about 1 in 4033, or 0.0248%.

Had it not been for teams playing each other, the odds would have been 1 in about 16,186. So the Ranger’s chances of making the playoffs are about 4 times better because of these teams playing against each other.

The Al Central tiebreaker that isn’t, but that is

tomisphereLeave a comment

The Cleveland Guardians haven’t secured the tiebreaker against the Detroit Tigers for the AL Central division title.

But they have.

What on Earth am I talking about?
Read on …

Right now the Tigers are one game ahead of the Guardians with 6 games left to play. It’s therefore very possible that they end up tied for the division lead. In that case, the division winner would be decided by a tiebreaker.

The tiebreaker is based on which team has won more games in their head-to-head matchups this season. The Guardians have won 6 of the 10 games played between them and the Tigers so far this year, and the Tigers have won 4. But there are 3 more to be played, and they’ll be played today through Thursday. Whichever team ends up with 7 or more wins against the other wins the tiebreaker between them.

So for Detroit to win the tiebreaker, they’ll need to win all three of the remaining games. But that would put Detroit 4 games ahead of Cleveland with only 3 games left to play in the season. Cleveland would not be able to make up that ground, so would not be able to win the division (not even by a tie and a tiebreaker).

The only way for a tie to come about this year is therefore if Cleveland wins at least one game against Detroit. And if that happens, Cleveland reaches the required 7 wins to hold the tiebreaker.

Basically, if the tiebreaker matters, then the Cleveland Guardians will hold it.

And that also means that whichever team wins this three game series between them, will find themselves in the lead for the division, just as was the case with the Seattle Mariners/Houston Astros series this past weekend.

And that makes the Guardians/Tigers series the most impactful series happening right now. Definitely one to keep an eye on!

The Toronto Blue Jays have about a 99.99987% chance of making the playoffs

tomisphereLeave a comment

There is a very very narrow range of circumstances under which the Toronto Blue Jays do not make the playoffs. So narrow, in fact, that if we assume every game remaining in the MLB this year has a 50% chance of being won by either team, the odds of the Blue Jays failing to make the playoffs are 1 about 793,072. That equates to a 99.999874% chance that they make the playoffs.

So how do we work out such numbers? Buckle up for a logic roller coaster ride.

To fail to get into the playoffs, every one of the Yankees, Red Sox, Mariners, Astros, Tigers, and Gaurdians would have to beat the Blue Jays, and these are the only 6 teams capable of surpassing the Blue Jays at this point.

At this point, the Blue Jays can end up with at most 73 losses, if they lose all 7 of their remaining games. So surpassing them would especially require a lot of winning by the Gaurdians and Astros (with 71 losses each currently) and the Red Sox and Tigers (with 70 losses each).

But these teams are limited in how much winning they can do the rest of the way, because there will be 6 games played between them. The Tigers and the Gaurdians will play 3 games against each other, and the Tigers and the Red Sox will play 3 against each other. That means there will be at least 6 losses spread around among those 3 teams.

So let’s consider the possible outcomes of the Tigers/Gaurdians series. For each outcome, let’s assume the Blue Jays lose all 7 of their remaining games, ending with a record of 89-73. Let’s also assume both the Tigers and the Gaurdians win all 4 of their other remaining games.

Except that we can’t assume that. Because if the Tigers win all their other 4 games, that means they deliver 3 losses to the Red Sox, who end up at best 89-73, the same as the Blue Jays. Because the Blue Jays end up with 7 wins and 6 losses against the Red Sox, they win the tiebreaker with the Red Sox and are in the playoffs. So the Tigers must lose a game to the Red Sox, and the Red Sox must win their other 4 games not against the Tigers, for the Blue Jays to have a chance at elimination here.

So we’ll assume the Tigers lose 1 more game (versus the Red Sox) outside of the Tigers/Gaurdians series, and the Guardians don’ t lose any others.

If the Gaurdians sweep the Tigers, the Tigers end up 88-74, a game behind the Blue Jays, and the Blue Jays are in the playoffs.

If the Tigers sweep the Guardians, the Gaurdians end up 88-74, a game behind the Blue Jays, and the Blue Jays are in the playoffs.

If the Gaurdians win 2 of 3, the Tigers end up 89-73, tied with the Blue Jays. Because the Blue Jays had 4 wins and 3 losses in their games against the Tigers this year, they win the tiebreaker between the teams, and are in the playoffs.

That leaves the scenario where the Tigers win 2 of 3. Then the Tigers end up 90-72, ahead of the Blue Jays, while the Guardians tie the Blue Jays at 89-73. So as a tiebreaker we look and see that the Blue Jays and Gaurdians each won 3 games against each other this year. We have to use the second tiebreaker, which is records within their own divisions. The Gaurdians end up 36 and 16 against their weaker division; the Blue Jays 25 and 27 against their stronger division. The Gaurdians therefore win this tiebreaker, and the Blue Jays are out of the playoffs – if the other 3 teams surpass them too, that is.

That’s the only scenario in which the Blue Jays are eliminated.

What if The Tigers lose one more game against another opponent? Then they end up with the same record as the Blue Jays, and the Blue Jays are in because they win the tiebreaker with the Tigers. So the Tigers must only lose the one game against the Red Sox.

That covers what must happen with the Tigers, Gaurdians, and Red Sox. What of the Yankees, Mariners, and Astros?

The Blue Jays hold the tiebreaker over the Yankees, so the Yankees must get to at least 90 wins, and therefore must win at least 3 of their last 7 games.

The Blue Jays hold the tiebreaker over the Mariners, so the Mariners must win at least 4 of their last 7 games.

The Astros hold the tiebreaker over the Blue Jays, so they must win at least 5 of their last 7 games.

So now we must get the odds of all these things happening and multiply them together to get the odds that the Blue Jays miss the playoffs. We assume in every game that the teams have an equal chance of winning. The following table contains all the odds:

The reason the Mariners and Astros are lumped together in the last line is that they play one more game against each other, so their odds of reaching their respective win totals are linked because of that game.

When you multiply all these odds together you get 693,198 divided by 2 to the 39th power, which is about 1 in 793,072, or 0.000126%. That’s the odds that they don’t make the playoffs; so the odds that they make the playoffs are about 99.999874%.